Radioactivity

In radioactive processes, particles or electromagnetic radiation are emitted from the nucleus. The most common forms of radiation emitted have been traditionally classified as alpha (a), beta (b), and gamma (g) radiation. Nuclear radiation occurs in other forms, including the emission of protons or neutrons or spontaneous fission of a massive nucleus.
Of the nuclei found on Earth, the vast majority are stable. This is so because almost all short-lived radioactive nuclei have decayed during the history of the Earth. There are approximately 270 stable isotopes and 50 naturally occurring radioisotopes (radioactive isotopes). Thousands of other radioisotopes have been made in the laboratory.
Radioactive decay will change one nucleus to another if the product nucleus has a greater nuclear binding energy than the initial decaying nucleus. The difference in binding energy (comparing the before and after states) determines which decays are energetically possible and which are not. The excess binding energy appears as kinetic energy or rest mass energy of the decay products.
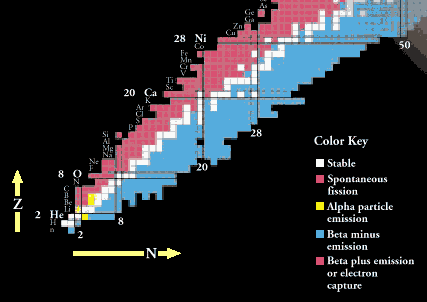
The Chart of the Nuclides, part of which is shown above is a plot of nuclei as a function of proton number, Z, and neutron number, N. All stable nuclei and known radioactive nuclei, both naturally occurring and manmade, are shown on this chart, along with their decay properties. Nuclei with an excess of protons or neutrons in comparison with the stable nuclei will decay toward the stable nuclei by changing protons into neutrons or neutrons into protons, or else by shedding neutrons or protons either singly or in combination. Nuclei are also unstable if they are excited, that is, not in their lowest energy states. In this case the nucleus can decay by getting rid of its excess energy without changing Z or N by emitting a gamma ray.
Nuclear decay processes must satisfy several conservation laws, meaning that the value of the conserved quantity after the decay, taking into account all the decay products, must equal the same quantity evaluated for the nucleus before the decay. Conserved quantities include total energy (including mass), electric charge, linear and angular momentum, number of nucleons, and lepton number (sum of the number of electrons, neutrinos, positrons and antineutrinos–with antiparticles counting as -1).
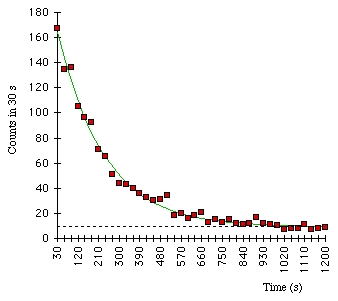
137Ba decay data, counting numbers of decays observed in 30-second intervals. The best-fit exponential curve is shown. The points do not fall exactly because of statistical counting fluctuations.
The probability that a particular nucleus will undergo radioactive decay during a fixed length of time does not depend on the age of the nucleus or how it was created. Although the exact lifetime of one particular nucleus cannot be predicted, the mean (or average) lifetime of a sample containing many nuclei of the same isotope can be predicted and measured. A convenient way of determining the lifetime of an isotope is to measure how long it takes for one-half of the nuclei in a sample to decay–this quantity is called the half-life, t1/2. Of the original nuclei that did not decay, half will decay if we wait another half-life, leaving one-quarter of the original sample after a total time of two half-lives. After three half-lives, one-eighth of the original sample will remain and so on. Measured half-lives vary from tiny fractions of seconds to billions of years, depending on the isotope.
The number of nuclei in a sample that will decay in a given interval of time is proportional to the number of nuclei in the sample. This condition leads to radioactive decay showing itself as an exponential process, as shown above. The number, N, of the original nuclei remaining after a time t from an original sample of N0 nuclei is
N = N0e-(t/T)
where T is the mean lifetime of the parent nuclei. From this relation, it can be shown that t1/2 = 0.693T.
Chapter Contents
|

