Three other symmetry principles important in nuclear science are parity P, time reversal invariance T, and charge conjugation C. They deal with the questions, respectively, of whether a nucleus behaves in a different way if its spatial configuration is reversed (P), if the direction of time is made to run backwards instead of forward (T), or if the matter particles of the nucleus are changed to antimatter (C). All charged particles with spin 1/2 (electrons, quarks, etc.) have antimatter counterparts of opposite charge and of opposite parity. Particle and antiparticle, when they come together, can annihilate, disappearing and releasing their total mass energy in some other form, most often gamma rays.
The changes in symmetry properties can be thought of as "mirrors" in which some property of the nucleus (space, time, or charge) is reflected or reversed. A real mirror reflection provides a concrete example of this because mirror reflection reverses the space direction perpendicular to the plane of the mirror. As a consequence, the mirror image of a right-handed glove is a left-handed glove. This is in effect a parity transformation (although a true P transformation should reverse all three spatial axes instead of only one).
Until 1957 it was believed that the laws of physics were invariant under parity transformations and that no physics experiment could show a preference for left-handedness or right-handedness. Inversion, or mirror, symmetry was expected of nature. It came as some surprise that parity, P, symmetry is broken by the radioactive decay beta decay process. C. S. Wu and her collaborators found that when a specific nucleus was placed in a magnetic field, electrons from the beta decay were preferentially emitted in the direction opposite that of the aligned angular momentum of the nucleus. When it is possible to distinguish these two cases in a mirror, parity is not conserved. As a result, the world we live in is distinguishable from its mirror image.
The figure above illustrates this situation. The direction of the emitted electron (arrow) reverses on mirror reflection, but the direction of rotation (angular momentum) is not changed. Thus the nucleus before the mirror represents the actual directional preference, while its mirror reflection represents a directional preference not found in nature. A physics experiment can therefore distinguish between the object and its mirror image.
If, however, we made a nucleus out of antimatter (antiprotons and antineutrons) its beta decay would behave in the same way, except that the mirror image in Fig. 5-1 would represent the preferred direction of electron emission, while the antinucleus in front of the mirror would represent a directional preference not found in nature.
The great physicist, Richard Feynman, told a story to illustrate this point: suppose you were in two-way contact with some alien species, but only by "telegraph" (i.e., light flashes or radio signals). The well known procedures of SETI (Search for Extraterrestrial Intelligence), starting with prime numbers and progressing to pictures, physics, and chemistry information could be used to develop a common language and arrive at a good level of communication. You could tell the alien how tall you are by expressing your height in mutually understood wavelengths of light. You could tell the alien how old you are as some large number of ticks of a light-frequency clock. Now you want to explain how humans shake hands when they meet, and you describe extending your right hand. "Wait a moment!" says the alien. "What do you mean by ‘right’?"
Until 1957 there would have been no way of answering that question. But now you could use the parity experiment shown in Fig. 5-1. You could tell the alien to turn the experiment until the electrons come out in the upward direction (the direction opposite gravity), and the front edge of the rotating nucleus will move from right to left or clockwise to make the angular momentum. This works because the parity violation of the weak interaction allows us, at a fundamental level, to distinguish right from left.
Feynman also had a punch line to this story. Suppose, after lots of communication you finally can go into space and meet your alien counterpart. If, as you approach one another, the alien extends its left hand to shake, watch out! He’s made of antimatter! This, of course, is because a parity violation experiment constructed of antimatter would give the opposite result.
If the mirror in Fig. 5-1 not only reversed spatial direction but also changed matter to antimatter, then the experiment in front of the mirror would look just like its mirror image. Changing both C and P preserves the symmetry and we call this CP symmetry. The separate violations of P symmetry and C symmetry cancel to preserve CP symmetry. These symmetry violations arise only from the weak interaction, not from the strong and electromagnetic interactions, and therefore shows up strongly only in beta decay.
There are fundamental reasons for expecting that nature at a minimum has CPT symmetry–that no asymmetries will be found after reversing charge, space, and time. Therefore, CP symmetry implies T symmetry (or time-reversal invariance). One can demonstrate this symmetry by asking the following question. Suppose you had a movie of some physical process. If the movie were run backwards through the projector, could you tell from the images on the screen that the movie was running backwards? Clearly in everyday life there would be no problem in telling the difference. A movie of a street scene, an egg hitting the floor, or a dive into a swimming pool has an obvious "time arrow" pointing from the past to the future. But at the atomic level there are no obvious clues to time direction. An electron orbiting an atom or even making a quantum jump to produce a photon looks like a valid physical process in either time direction. The everyday "arrow of time" does not seem to have a counterpart in the microscopic world–a problem for which physics currently has no answer.
Until 1964 it was thought that the combination CP was a valid symmetry of the Universe. That year, Christenson, Cronin, Fitch and Turlay observed the decay of the long-lived neutral K meson, 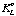 , to p + + p -. If CP were a good symmetry, the
, to p + + p -. If CP were a good symmetry, the 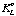 would have CP = -1 and could only decay to three pions, not two. Since the experiment observed the two pion decay, they showed that the symmetry CP could be violated. If CPT symmetry is to be preserved, the CP violation must be compensated by a violation of time reversal invariance. Indeed later experiments with K 0 systems showed direct T violations, in the sense that certain reaction processes involving K mesons have a different probability in the forward time direction (A + B Æ C + D) from that in the reverse time direction (C + D Æ A + B). Nuclear physicists have conducted many investigations searching for similar T violations in nuclear decays and reactions, but at this time none have been found.
would have CP = -1 and could only decay to three pions, not two. Since the experiment observed the two pion decay, they showed that the symmetry CP could be violated. If CPT symmetry is to be preserved, the CP violation must be compensated by a violation of time reversal invariance. Indeed later experiments with K 0 systems showed direct T violations, in the sense that certain reaction processes involving K mesons have a different probability in the forward time direction (A + B Æ C + D) from that in the reverse time direction (C + D Æ A + B). Nuclear physicists have conducted many investigations searching for similar T violations in nuclear decays and reactions, but at this time none have been found.
This may change soon. Time reversal invariance implies that the neutron can have no electric dipole moment, a property implying separation of internal charges and an external electric field with its lines in loops like Earth’s magnetic field. Currently ultracold neutrons are being used to make very sensitive tests of the neutron’s electric dipole moment, and it is anticipated that a nonzero value may be found within the next few years.

