
|
The Isotopes of Hydrogen

It is often useful to study the simplest system. Therefore, hydrogen, the simplest nucleus, has been studied extensively. The isotopes of hydrogen show many of the effects found in more complicated nuclei. (The word isotope refers to a nucleus with the same Z but different A).
There are three isotopes of the element hydrogen: hydrogen, deuterium, and tritium. How do we distinguish between them? They each have one single proton (Z = 1), but differ in the number of their neutrons. Hydrogen has no neutron, deuterium has one, and tritium has two neutrons. The isotopes of hydrogen have, respectively, mass numbers of one, two, and three. Their nuclear symbols are therefore 1H, 2H, and 3H. The atoms of these isotopes have one electron to balance the charge of the one proton. Since chemistry depends on the interactions of protons with electrons, the chemical properties of the isotopes are nearly the same.
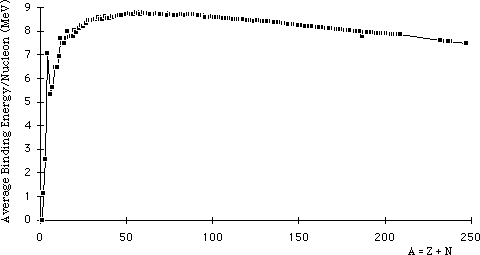
The curve of the average binding energy per nucleon.
Energy may be released as a packet of electromagnetic radiation, a photon. Photons created in nuclear processes are labeled gamma rays (denoted by the Greek letter gamma, g. For example, when a proton and neutron combine to form deuterium, the reaction can be written 1n + 1H Æ 2H + g. Energy must balance in this equation. Mass can be written in atomic mass units (u) or in the equivalent energy units of million electron-volts divided by the square of the speed of light (MeV)/c2. (From Einstein’s mass-energy equivalence equation, E = mc2, u = 931.5 MeV/c2.) The mass of the deuterium nucleus (2.01355 u) is less than the sum of the masses of the proton (1.00728 u) and the neutron (1.00866 u), which is 2.01594 u. Where has the missing mass (0.00239 u) gone? The answer is that the attractive nuclear force between the nucleons has created a negative nuclear potential energy–the binding energy EB–that is related to the missing mass, D m (the difference between the two masses). The photon released in forming deuterium has an energy of 2.225 MeV, equivalent to the 0.00239 u required to separate the proton and neutron back into unbound particles. The nuclear decay photons are, in general, higher in energy than photons created in atomic processes.
When tritium is formed by adding a neutron to deuterium, 1n + 2H Æ 3H+ g, a larger amount of energy is released–6.2504 MeV. The greater binding energy of tritium compared to deuterium shows that the nuclear potential energy does not grow in a simple way with the addition of nucleons (the total binding energy is roughly proportional to A). The binding energy per nucleon continues to grow as protons and neutrons are added to construct more massive nuclei until a maximum of about 8 MeV per nucleon is reached around A = 60, past which the average binding energy per nucleon slowly decreases up to the most massive nuclei, for which it is about 7 MeV.
How does a nucleus, which can have up to approximately 100 protons, hold itself together? Why does the electrical repulsion among all those positive charges not cause the nucleus to break up? There must be an attractive force strong enough to be capable of overcoming the repulsive Coulomb forces between protons. Experiment and theory have come to recognize an attractive nuclear interaction that acts between nucleons when they are close enough together (when the range is short enough). The balance between electromagnetic and nuclear forces sets the limit on how large a nucleus can grow.
|
|

