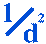
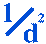
EXPERIMENT #1:
THE INVERSE SQUARES
Introduction
While using photographic film and sources similar to radium and uranium, Henri Becquerel discovered radiation in 1896. The following experiment will use a completely safe beta b particle of radiation (Strontium-90).
We have learned that radiation travels in all direction in straight lines from the center of the source like rays from the Sun. As the radiation moves farther from the source, it becomes less intense. With this information, we also know that the inverse square law applies accurately only when the distance from the source is several times greater than the diameter of the detector. In this experiment the distances are 8 cm, 16 cm, 24 cm, and 32 cm from the source. Data point one equals 8 cm, data point two equals 16 cm, and so on.
Objective
To explore and calculate (if any) the relationship between the distance from radioactive sources and the intensity of beta radiation.

Materials
- Geiger counter
- rail tracker
- Sr-90 (beta source)
- stop watch/beeper
- counting paper or hand counter
- graph paper
Procedure
- Place beta radiation source into hole on wooden block of rail tracker.
- Set the digital Geiger counter to one minute intervals and turn the power on. Allow the instrument to warm up for a few minutes.
- Record background activity.
- Place the counter on the slider, 8 cm from the beta source.
- Record counts per minute (cpm) in Table 1.1 for each trial and calculate the average.
- Move Geiger counter and slider to 16 cm from the source. Repeat step 6.
- Move Geiger counter to 24 cm and repeat step 6.
- Move Geiger counter to 32 cm and again repeat step 6.
- Calculate the uncertainty as the square root of the number of counts. Make sure you add the number of counts, take the square root and then divide by the total time. Record the calculation in column 8 of the Data Table. The plus or minus of this number will indicate the standard error of the experiment.
Data
|
Distance (cm)
|
Data Points
|
r2
|
Trial 1
|
Trial 2
|
Trial 3
|
Average (cpm)
|
Uncertainty
|
(1/r2) average count of 1st data point
|
|
8
|
1
|
1
|
|
|
|
|
|
|
|
16
|
2
|
4
|
|
|
|
|
|
|
|
24
|
3
|
9
|
|
|
|
|
|
|
|
32
|
4
|
16
|
|
|
|
|
|
|
- Graph the activity readings (cpm) vs. distance.
- Graph the activity readings (cpm) vs. 1/r2.
Questions
- Why was the background activity recorded for this experiment?
- What is the source of the background activity?
- Would the background activity be the same taken at sea level as taken on top of a mountain? EXPLAIN.
- What happens to the intensity of beta activity when the distance between the Geiger counter and source is four times as great as the initial distance? Three times as great?
- According to the inverse square law, when the distance is doubled from 8 cm to 16 cm the reading should decrease to 1/4 its initial reading. Do your data calculations agree with the inverse square? Explain why or why not.
- Explain how distance and radioactive materials are potential hazards to you.
- Interpolate the number of counts for the beta source at a distance of 12 cm.
Going Further
- Evaluate how background activities may influence your data.
This document was produced by the Nuclear Science Division of the Lawrence Berkeley National Laboratory.
![]()
![]()