Desperately Seeking SUSY:
What SUSY Can't Answer
Not only the heaviest but the lightest particles frustrate theory. Physicists hot on the
trail of the neutrino's mass must depend on experiments—in deep mines, under the
ocean, even under the subarctic ice—to supply the answers. Even SUSY can't explain
such things as the origin of the three families of quarks and leptons and why these
particles have a particular range of masses. This is a job for superstrings.
"The spectrum of states of a high-tension string give rise to all the particles we
observe," says Gaillard. Just as a violin string vibrating at different frequencies
and at different tensions sounds different musical notes, the vibrations of a tiny
superstring give rise to what we see as point-like particles with different masses and
different quantum numbers. There are so many possible vibrational states of superstrings
that all the particles ever observed are represented, and vastly more as well.
"Observed particles represent only the lowest energy states of superstrings,"
Gaillard says.
Extra dimensions give strings their explanatory power. As far back as 1919, the
mathematician Theodor Kaluza added a single dimension to Einstein's four-dimensional
spacetime—a dimension so small as to be invisible, somewhat as a tangle of garden
hose looks from a distance like a two-dimensional scribble—as a way of unifying
electromagnetism with gravity. In the 1960s, strings vibrating in 26 dimensions (25 of
space, one of time) were proposed to account for the strong nuclear force; this theory,
which was not a supersymmetric theory, was abandoned partly because it gave rise to a
mysterious massless, spin-two particle—only later identified, in the supersymmetric
version of string theory with nine space dimensions and one time dimension, as a possible
quantum of gravitation.
While it is easy to imagine short lengths or loops of string vibrating in
three dimensions—even wrapping themselves around spheres and toruses—it is
beyond humans to visualize nine spatial dimensions. Luckily we don't have to; the extra
dimensions are associated with each vibrating string at the invisibly tiny Planck scale,
so that a string in its compactified dimensions appears point-like to our experimental
apparatus. But, Gaillard emphasizes, "These rolled-up dimensions are real."
Nine-plus-one is not an arbitrary number of dimensions. It is the number for which the
theory is internally consistent and and turns out to have enough modes of a vibrating
string to manifest the forces we observe. Thus superstring theories possess both quantum
and geometric aspects, and they naturally unify all the known forces of nature. The
problem for experimentalists is that this unification, along with much else explained by
superstrings, can exist only at energies typical of the first infinitesimal fraction of a
second of the Big Bang.
|
[Above] As temperature
decreases, a plasma of dissociated hydrogen and oxygen nuclei and electrons may condense
to water vapor, and the vapor may cool to liquid water, and the liquid may cool to solid
ice.
|
|
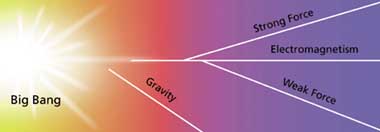
[Above] The four forces
governing the interactions of matter and energy "condensed" from the
unimaginable temperature and density of the Big Bang—gravity first, followed by the
strong nuclear force and the electroweak force, which yielded the familiar electromagnetic
force and the weak force that gives rise to radioactive decay. All but gravity can be
linked by extensions of the Standard Model.
|
Wiggling it to make it fit
The smaller the scale, the more energy required to study it, and superstrings are small
indeed, two-dimensional objects some 20 orders of magnitude smaller than a proton, a
billion-trillion-trillionth of a centimeter. No accelerator will ever be able to study
superstrings directly, but that doesn't mean evidence is impossible to come by. The key is
to make use of a mathematical technique known as perturbation theory. Until recently there
were five distinct versions of superstring theory, but it is now thought that all five may
describe the same physics under different conditions; all five may be manifestations of a
single underlying theory, known as M theory (wags have suggested that M stands for
"magic"). In addition to strings, M theory posits even higher-dimensional
entities known as Dirichlet membranes, or D-branes—and it permits the study of
previously inaccessible, non-perturbative phenomena by perturbative methods. The most
promising versions of SUSY are perturbative over a wide range of energies, which means
that the behavior of the constituent particles can be accurately predicted by making small
adjustments to straight forward calculations. Perturbation theory allows the results of
low-energy experiment to be extrapolated and compared with the predictions of high-energy
theory. If superparticles are found, it will be encouraging evidence for superstrings. One
of the things string theorists like best about SUSY is that their theories require it; the
"super" in superstrings comes from this association. John Schwartz, a string
theorist notable for his enthusiasm, writes that to find supersymmetry "would be one
of the most profound achievements in the history of mankind... more profound, in my
opinion, than the discovery of life on Mars"—because it would imply that at
least some version of superstring theory is correct. Gaillard's favorite version has an
intriguing form which includes two groups of terms. "One describes our world,"
she says, "and perhaps the other describes a shadow world. That's one of things I'm
working to find out."


