Now, collaborators at the Department of Energy's Lawrence Berkeley National Laboratory, Lawrence Livermore National Laboratory, and the University of California at Davis have used supercomputers to obtain a complete solution of the ionization of a hydrogen atom by collision with an electron, the simplest nontrivial example of the problem's last unsolved component. They report their findings in the 24 December, 1999, issue of Science magazine.

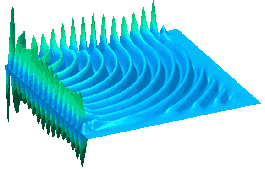
A REPRESENTATIVE RADIAL WAVE FUNCTION OF TWO ELECTRONS SCATTERED IN THE COLLISION OF AN ELECTRON WITH A HYDROGEN ATOM

Their breakthrough employs a mathematical transformation of the Schrödinger wave equation that makes it possible to treat the outgoing particles not as if their wave functions extend to infinity -- as they must be treated conventionally -- but instead as if they simply vanish at large distances from the nucleus.

"Using this transformation we compute accurate solutions of the quantum-mechanical wave function of the outgoing particles, and from these solutions we extract all the dynamical information of the interaction," says Bill McCurdy, Berkeley Lab's Associate Laboratory Director for Computing Sciences and a principal author of the Science article.

McCurdy and his longtime collaborator Thomas Rescigno, a staff physicist at Livermore Lab, and their co-authors, doctoral candidate Mark Baertschy of UC Davis and postdoctoral fellow William Isaacs at Berkeley Lab, used the SGI/Cray T3E at the National Energy Research Scientific Computing Center (NERSC) at Berkeley Lab and the IBM Blue Pacific computer at Livermore Lab for their solution of the three-charged-body scattering problem.

"An exact first-principles solution of the wave function for the hydrogen atom was vital to establishing the new quantum theory in the 1920s," says Rescigno. "But even today, for systems with three or more charged particles, no analytic solutions exist" -- that is, there are no explicit solutions to the Schrödinger equation for such systems.

Rescigno points out that "it wasn't until the late 1950s, using early computers, that accurate solutions were obtained even for the bound states of helium," an atom with two electrons closely orbiting the nucleus. "Scattering problems are a lot more difficult."

As with all scattering problems, the electron-ionization of a hydrogen atom begins with a particle incoming at a certain velocity. This electron interacts with the atom, and two electrons fly out at an angle to each other, leaving the proton behind. The likelihood that a specific incoming state will result in an outgoing state with the particles at specific angles and energies is the "cross section" for that result.

Cross sections of quantum-mechanical processes are derived from the system's wave function, solutions of the Schrödinger equation which yield probabilities of finding the entities involved in a certain state. In scattering problems, wave functions are not localized but extend over all space.

Moreover, says McCurdy of the electromagnetic forces between charged particles, "Coulomb interactions are forever." These infinities make it impossible to define the final state of scattering exactly. "The form of the wave function where all three particles are widely separated is so intractable that no computer-aided numerical approach has been able to incorporate it explicitly."

But, Rescigno notes, "this obviously hasn't stopped people from working with plasmas and other ionization phenomena. Mathematically, they've come up with incredibly artful dodges, and some of them even seem to work."

Earlier this year, however, in the Proceedings of the Royal Society, Colm T. Whelan of Cambridge University and his colleagues published their conclusion that all such approximations perform inconsistently and that those few cases which appear to yield good agreement with experiment "are largely fortuitous."

By contrast, the method developed by McCurdy and Rescigno and their co-authors allows the calculation of a highly accurate wave function for the outgoing state that can be interrogated for details of the incoming state and interaction in the same way an experimenter would interrogate a physical system.

They begin with a transformation of the Schrödinger equation called "exterior complex scaling," invented by Caltech's Barry Simon in 1979 to prove formal theorems in scattering theory. The transformation leaves the solution unchanged in regions which correspond to physical reality, producing the correct outgoing waveform based upon the angular separation and distances of two electrons far from the nucleus.

Once the wave function has been calculated, it must be analyzed by computing the "quantum mechanical flux," a means of finding the distribution of probability densities that dates from the 1920s. This computationally intensive process can yield the probability of producing electrons at specific energies and directions from the ionized atom. (Because electrons are identical, there is no way to distinguish between the initially bound and initially free electron).

The researchers acknowledge important advances made earlier by others such as Igor Bray and Andres Stelbovics, whose methods could give the total cross section for ionization of a scattering reaction but could not give specifics such as the directions or energies of outgoing electrons. By contrast, says Rescigno, "Our work produces absolute answers at the ultimate level of detail."

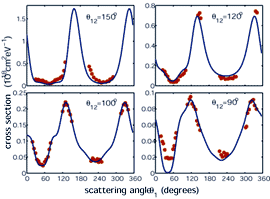
PREDICTED CROSS SECTIONS OF SCATTERED ELECTRONS (SOLID CURVES) AND EXPERIMENTAL MEASUREMENTS (DOTS) MATCH ALMOST EXACTLY

Comparison with real scattering experiments, such as those recently published by J. Röder et al, who scattered incoming 17.6 electron-volt electrons from hydrogen atoms and measured the angles and energies of the outgoing electrons, prove the accuracy of the new method. The experimental data points match the graph of the cross sections calculated by Rescigno, Baertschy, Isaacs, and McCurdy with astonishing exactitude.

"Even if the specific methods have changed, quantum chemistry was founded when the helium atom with two bound electrons was solved -- it showed that these problems were in principle solvable," McCurdy says. "What we have done is analogous. The details of our method probably won't survive, but we've taken a big step toward treating ionizing collisions of electrons with more complicated atoms and molecules."

"Collisional breakup in a quantum system of three charged particles," by T.N. Rescigno, M. Baertschy, W.A. Isaacs, and C.W. McCurdy appears in Science magazine, 24 December 1999. The authors conclude by noting that the same computing power and tools necessary for investigating the complexity of increasingly larger systems are also needed "to answer a basic physics question for one of the simplest systems imaginable in physics and chemistry."

The Berkeley Lab is a U.S. Department of Energy national laboratory located in Berkeley, California. It conducts unclassified scientific research and is managed by the University of California.