Shape Changes in Ceramic Particles: A Paradox Explained |
 |
|
By Paul Preuss, paul_preuss@lbl.gov December 2, 1997 |
BERKELEY, CA -- A long-standing paradox in the theory of sintering ceramics has been resolved by Alan W. Searcy of the Materials Sciences Division at the Ernest Orlando Lawrence Berkeley National Laboratory. Searcy's work, done in collaboration with Jeffrey Bullard of the University of Illinois and W. Craig Carter of the National Institute of Standards and Technology, promises to shed light on the properties of many ceramics, including layered semiconductors and heat-resistant silicon nitrides.
In sintering, one of the most important processes in ceramics manufacture, fine-powder compacts are heated to temperatures only a little lower than their melting points; atoms and molecules are set in rapid motion, and the particles coalesce, reducing porosity and increasing the strength of the finished product.
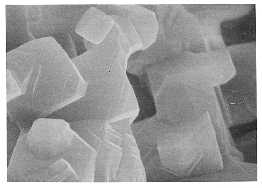
At top, particles of lithium fluoride retain facets during sintering (at 680 degrees Celsius in vacuum.) In the bottom image, sintered particles which appear rounded would also reveal facets if seen at higher magnification. (Shown are lithium fluoride particles heated to 680 degrees Celsius in argon.)
The "classical" approach to sintering assumes that the initial particles in the compact are spheres and that movements of atoms or molecules are driven by differences in curvature. In order to reduce surface free energy (the work required to form a surface), atoms supposedly move from particles of smaller radius to particles of larger radius; the concave regions formed by contact between particles are filled by atoms from convex surfaces.
In fact, the molecules of crystalline particles sometimes move in directions the theory forbids -- "Which is not surprising," Searcy remarks, "because the classical theory fails what I think of as the 'single-particle sintering test.' It predicts that an isolated particle of arbitrary shape will evolve into a sphere. On the contrary, most single crystals, if grown slowly enough, are faceted." Unlike an idealized sphere, the surface energies of a crystal depend on the different orientation of the surfaces to the underlying crystal-lattice structure.
"So here's a theory that says you can't get sintering with particles that have planar surfaces and edges," Searcy says, "while in fact many solids, such as magnesium oxide, cobalt oxide, sodium chloride, and lithium fluoride, keep their faceted shapes -- or even grow into faceted shapes -- while they are being sintered."
A clue to the puzzle came when Searcy read a footnote in the work of Josiah Willard Gibbs, the nineteenth-century founder of chemical thermodynamics. Gibbs pointed out that molecules at the edges between crystalline facets would leave and return to their crystal sites more often than molecules in the facet surfaces, because the edge molecules are less strongly bonded.
Inspired by what he calls Gibbs's "qualitative description of dynamic equilibrium," Searcy worked with Bullard and Carter, both former students at LBNL, to develop equations that explain shape changes during sintering in terms of energy differences among differently oriented surfaces and edges -- "rate equations" founded on Searcy's "statistical thermodynamic description of the unstable internal equilibrium" in crystals of any shape.
The new equations are based on two governing principles: first, any change in shape is possible if it reduces total energy -- the change need not minimize energy, merely reduce it. Second, among all possible shape changes, the one that actually occurs is the one in which the exchange of atoms or molecules and vacant crystal lattice sites is easiest -- the one most favored kinetically.
The new equations make it plain that particles don't grow faster because they are curved; instead the apparent curves are produced by the growth of new crystal layers. "Rounded" edges which appear during sintering are actually small additional facets -- kinetically favored to grow because it is easier to move atoms or molecules to those sites. As these small, fast-growing facets multiply, particles begin to appear classically rounded, but become faceted again in the final stages of sintering.
For example, if two cubic crystals of magnesium oxide are in contact with each other, the smaller rapidly transforms into a nearly spherical particle. A rounded neck forms between it and the larger particle, which is still nearly cubic -- producing a sort of lopsided dumbbell. Given enough time, a single large cube with slightly rounded edges will form. At every step the changes serve to balance the demands of minimum surface energy; only changes which reduce energy are allowed.
Recently Searcy, Bullard, and Carter used Searcy's model to solve a puzzle reported by Oak Ridge researchers. Observed in a transmission electron microscope (TEM), box-like particles of magnesium oxide slowly grew connecting necks during over two hours of sintering -- then in 20 minutes the necks collapsed and disappeared.
Three thermodynamic pathways were suggested by the new equations, one of which matched the observations exactly by taking into account the chemical reaction of the magnesium oxide particles with the supposedly unreactive carbon substrate on which they were mounted. In the vacuum chamber of the TEM, carbon and magnesium oxide react to release carbon monoxide and magnesium vapor, reducing the overall energy of the magnesium-oxygen-carbon system.
Searcy is now extending his model to study the thermodynamics of films on and between solid surfaces, work which promises to illuminate production methods and properties of such ceramics as layered semiconductors and strong, tough, high-temperature engine parts made with silicon nitride particles separated by glass films only a billionth of a meter thick.
Searcy and Bullard report confirmation of a prediction of the new model in the Journal of the American Ceramic Society, September 1997: cubic particles of lithium fluoride sinter as readily as spherical particles of other ceramics.
The Berkeley Lab is a U.S. Department of Energy national laboratory located in Berkeley, California. It conducts unclassified scientific research and is managed by the University of California.

