BERKELEY -- A team of theorists at the Department of Energy's Lawrence
Berkeley National Laboratory, whose calculations motivated the successful synthesis of
materials based on carbon-36 fullerenes, has calculated that these systems may lose all
electrical resistance at temperatures far higher than any other carbon structure --
perhaps even at temperatures in the range that superconducting copper-oxide ceramics have
achieved.
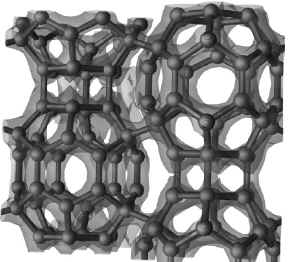
Carbon-36 fullerenes bond tightly in a hexagonal
crystal
|
"The highest- temperature superconductor is the home run that everybody is trying
to hit," says Marvin Cohen, who with Steven G. Louie heads a theory group in Berkeley
Lab's Material Sciences Division (MSD); both are professors of physics at the University
of California at Berkeley. "Even if the carbon-36 materials don't achieve this, they
give us a new class of solids to help develop our knowledge about this field."
Cohen says, "If you intercalate potassium atoms among the planes of graphite, even
graphite becomes superconducting -- but at half a degree Kelvin," an inconveniently
low temperature. "On the other hand, C-60 'buckyballs' doped with alkali metals can
be superconductors at up to 40 K. Part of the explanation seems to be the curvature of the
ball."
A closed carbon structure with more overall curvature than C-60 is expected to have
fewer atoms; while fullerenes smaller than C-60 have been observed, experimenters Charles
Piskoti, Alex Zettl, and Jeff Yarger of UC Berkeley, who are also with Berkeley Lab's MSD,
were the first to extract an appreciable amount of C-36, having been encouraged by the
Cohen-Louie group's theoretical calculations. The Zettl group announced the isolation of
bulk samples of C-36 in Nature on 25 June, 1998.
Graduate student Michel Côté and postdoctoral fellow Jeffrey C. Grossman of the
Cohen-Louie group emphasize the value of their close working relationship with Zettl's
experimental group. "The cross fertilization has helped us all," says Grossman.
Long ago, the 18th century mathematician Leonhard Euler established that every closed
polygon made with hexagons and pentagons must contain exactly 12 pentagons. C-60's
soccer-ball shape is the smallest possible structure in which the 12 do not touch; in any
smaller structure, the pentagons must touch.
Indeed, the likeliest structure incorporating 36 carbon atoms consists of two
"bowls," each a hexagon surrounded by six pentagons; each bowl has 18 vertices
where atoms sit. The two pentagon-sided bowls face each other, forming an equatorial belt
of six more hexagons.
The resulting structure has so-called D6h symmetry, meaning that if it is rotated
around its long axis, it looks the same after each sixth of a turn, and if it is sliced
through the equator, its top and bottom are identical. A carbon atom in the D6h structure
may have one of three different bonding configurations, depending on its relation to its
neighbors. Thus C-36 has what Grossman calls "three unique atoms."
Côté says, "The strain on the bonds among atoms influences electron-phonon
coupling, and according to BCS theory" -- advanced in 1957 by John Bardeen, Leon
Cooper, and Robert Schriefer to explain superconductivity in terms of the motion of
electron pairs -- "electron-phonon coupling is a mechanism that makes
superconductivity possible."
Phonons are a way of representing atomic vibrations in a solid; oscillations in
interatomic charge can make it possible for electrons to move as pairs. Strained or
"bent" bonds between carbon atoms in fullerenes may expose electron orbitals
normally unaffected by the vibrational modes in flat graphite. The more electron orbitals
the atomic vibrations can affect, the greater the potential for electron-phonon coupling
and the greater the prospects for superconductivity.
Carbon atoms at the vertices of a pentagon are under more strain than those at the
vertices of a hexagon. Moreover, "clustering of pentagons creates severely strained
atomic sites," says Côté. Every atom in the D6h structure is at the vertex of one
or two pentagons.
Although Côté and Grossman did their calculations on individual molecules first,
"which electrons couple depends on how the molecules form a solid," Grossman
says. If the D6h fullerenes are arranged in a repeating crystal lattice, two close-packed
arrangements are possible: the hexagonal, in which each molecule sits directly over
another, and the rhombohedral, in which each molecule perches midway between the molecules
below it.
Working with colleagues at Berkeley Lab's National Energy Research Scientific Computing
Center, Côté and Grossman used the pseudopotential method pioneered by Marvin Cohen in
calculating the electronic densities and other properties of the two crystals. They
calculated that the rhombohedral crystal would be metallic and that the hexagonal crystal,
which is slightly favored energetically, would be an insulator. A striking difference
between C-36 crystals and those of C-60 is that C-36 molecules are covalently bonded --
much more tightly bound than buckyballs in a crystal.
Côté and Grossman estimated the electron-phonon coupling for these solids and -- by
making the plausible assumption that certain factors are the same as for C-60 -- found
that the temperature at which solid C-36 becomes superconducting could be as much as three
times higher. Not room temperature, exactly -- but plenty hot enough to encourage further
investigation of this new material.
"However," says Grossman, "the superconducting temperature depends on
other factors besides the electron-phonon coupling, so it's hard to make quantitative
predictions from theory."
While preliminary results indicate the possibility of raising the superconducting
temperature of C-36 above the boiling point of nitrogen, 77 degrees Kelvin, whether it can
be raised even higher -- above that of the present record-holder, which at ambient
pressure becomes superconducting at 135 degrees Kelvin -- is uncertain.
To resolve these uncertainties, Côté and Grossman are extending and continuing their
calculations. In the meantime, they emphasize the implications of their latest theoretical
work for the progress of materials science.
"We're no longer saying, 'Here's a model of something you may never see',"
says Grossman. "Because of increased computing power and highly developed algorithms,
we can now construct realistic physical models and then make predictions from first
principles about real materials which can be made."
"We were able to tell the experimenters in advance that a C-36 cystal should
form," Côté adds, "and by specifying different properties, we could help them
decide which form they had made."
Côté, Grossman, Cohen, and Louie discuss their investigation of electron-phonon
interactions in solid C-36 in Physical Review Letters, July 20,
1998, and the structure and properties of molecular C-36 in Chemical Physics
Letters, March 6, 1998.
The Berkeley Lab is a U.S. Department of Energy national laboratory located in
Berkeley, California. It conducts unclassified scientific research and is managed by the
University of California.