At the Advanced Light Source, robots precisely mount tiny protein crystals in crystallography beamlines.

To learn more about life, Berkeley Lab researchers rely on robots. They've automated a traditionally slow process in which tiny protein crystals are mounted and centered in an x-ray beam and analyzed for their molecular structure.

The robot, which is the first such device available to general users at a synchrotron, both mounts protein crystals in a beamline and uses the resulting data to decipher the protein's atomic makeup. Once fully implemented, it will facilitate a ten-fold increase in the number of proteins mapped annually at Berkeley Lab's Advanced Light Source (ALS), the world's brightest source of ultraviolet and x-ray light. Such super-charged throughput is needed to keep pace with the mountains of data produced by genome sequencing and drug development research.

At Beamline 5.0, researchers can determine the structure of proteins from protein crystals only a few tens of millionths of a meter in size. (Photo: NASA)

"When it comes to synchrotrons, there is more demand than supply," says Thomas Earnest of Berkeley Lab's Physical Biosciences Division.

Synchrotrons work by accelerating electrons to nearly the speed of light and bending them in a circular path by powerful magnets. At this speed, electrons emit extremely bright x-ray light that is directed along a beamline toward an object that researchers want to investigate at the atomic level -- in this case protein crystals. The pattern in which x-rays diffract off of the crystal is used to determine the protein's molecular structure, which in turn is used to deduce the protein's function.

It's a laborious process. By hand, it takes roughly 10 to 20 minutes to mount and align a protein crystal in a beamline. At this pace, it would take years to muddle through the more than 30,000 proteins produced by the human genome. People just aren't cut out for many of the repetitive, round-the-clock tasks that comprise the protein-by-protein inquiry into how genes function.

	Electron density map of a ribosomal structure determined at the ALS (Noller, UC Santa Cruz)

But machines love repetition. Earnest and colleagues' industrialized approach to the data-acquisition phase of protein crystallography features a container that houses 112 protein crystals. Nitrogen gas cryogenically cools the crystals to about 100 Kelvin, an extremely low temperature that must be maintained throughout the process in order to minimize radiation damage.

Using a computer, an operator selects the crystals to be studied, and a cryogenically cooled arm dips into the container, mounts a crystal on a thin filament loop in about ten seconds, and centers it in the beamline. A series of test exposures ensures that the crystal is both optimally positioned and pure enough to provide reliable data. If everything checks out, the robot obtains a full set of x-ray data. The entire process takes only about two minutes per crystal -- and the result is enough data to piece together a three-dimensional rendering of the protein's molecular building blocks.

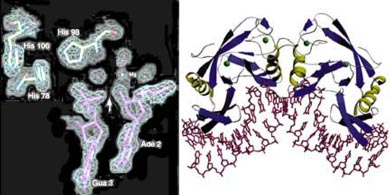
An enzyme's structural data from the ALS (left) yields a diagram of its protein structure (right). (Stoddard, Fred Hutchinson Cancer Center)

The robot was developed by the Lab's Berkeley Center for Structural Biology instrumentation group in collaboration with the Engineering Division's bioinstrumentation group. It has been available to general users at ALS beamline 5.0.3 since last summer and so far has helped analyze roughly 2,000 user-provided proteins. Earlier this year, a second robot was installed on beamline 5.0.2, and two more are slated for installation in the near future. In addition, Berkeley Lab researchers are helping to replicate the system at Brookhaven National Lab's National Synchrotron Light Source and Cornell University's High Energy Synchrotron Source.

In keeping with the robot's faster-is-better imperative, Earnest hopes to soon add smart software that evaluates the data as it's collected, and uses this feedback to constantly refine the data collection process and how the crystals are chosen. This project is conducted in collaboration with the Physical Biosciences Division's Computational Crystallography Initiative.

In addition, crystal characteristics will be prescreened and fed to the robot via a server. This data will enable the robot to more quickly zero in on crystal-specific variables such as the optimal distance between the crystal and the x-ray detector, and the angular range at which the data is collected. This circumvents time-consuming trial-and-error steps and further automates the process.

"The idea is crystals in, structures out," Earnest says. "Ultimately, we would like to place 112 crystals in the container and walk away."

Another time-saver already in use is the so-called "hockey puck," a cylindrical cassette that holds 16 protein crystals. Seven pucks fit inside a standard shipping container, and the same number can be nestled in the robot's cryogenically cooled container. This means outside users can prepare 112 protein samples and send them to the ALS, where they can be quickly transferred to the robot for analysis.

Earnest cautions that automating the beamline phase of protein crystallography isn't the only hurdle. Other bottlenecks remain, such as protein production and crystallization. Even so, the robot is a critical component in the push to increase the amount of structural information a beamline can produce, he says.

In addition to basic research, the robot is also expected to help speed drug development. Pharmaceutical companies are currently researching the therapeutic effects of hundreds of enzymes and peptides that bind with proteins. Understanding just how these compounds bind -- a process that can be best visualized with x-ray diffraction -- will enable companies to develop better pharmaceuticals. So the quicker companies can funnel promising drug candidates through beamline analysis, the quicker they can get them to consumers.

"Ultimately, we want to go from sequence to protein structure to function, and the robot will help us to that," Earnest says. "This saves the human brain for tasks it's better suited for, such as wondering just how proteins work."

Additional information:

• More about protein crystallography at beamline 5.0