
|
The Shell Model

One such model is the Shell Model, which accounts for many features of the nuclear energy levels. According to this model, the motion of each nucleon is governed by the average attractive force of all the other nucleons. The resulting orbits form "shells," just as the orbits of electrons in atoms do. As nucleons are added to the nucleus, they drop into the lowest-energy shells permitted by the Pauli Principle which requires that each nucleon have a unique set of quantum numbers to describe its motion
.
When a shell is full (that is, when the nucleons have used up all of the possible sets of quantum number assignments), a nucleus of unusual stability forms. This concept is similar to that found in an atom where a filled set of electron quantum numbers results in an atom with unusual stability–an inert gas. When all the protons or neutrons in a nucleus are in filled shells, the number of protons or neutrons is called a "magic number." Some of the magic numbers are 2, 8, 20, 28, 50, 82, and 126. For example, 116Sn has a magic number of protons (50) and 54Fe has a magic number of neutrons (28). Some nuclei, for example 40Ca and 208Pb, have magic numbers of both protons and neutrons; these nuclei have exceptional stability and are called "doubly magic." Magic numbers are indicated on the chart of the nuclides.
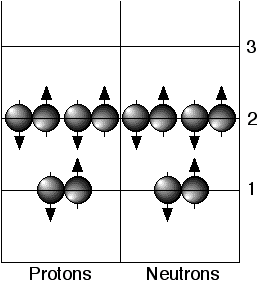
Filled shells have a total angular momentum, J, equal to zero. The next added nucleon (a valence nucleon) determines the J of the new ground state. When nucleons (singly or in pairs) are excited out of the ground state they change the angular momentum of the nucleus as well as its parity and isospin projection quantum numbers. The shell model describes how much energy is required to move nucleons from one orbit to another and how the quantum numbers change. The figure above shows an energy diagram of the two filled shells of the ground state of 12C. Promotion of a nucleon or a pair of nucleons to an unfilled shell puts the nucleus into one of the excited states.
Excited nuclear states decay to more stable states, i.e., more stable nucleon orbitals. Measuring transition rates between nuclear energy levels requires specialized alpha, beta, and gamma detectors and associated electronic circuitry to precisely determine the energy and half-life of the decay. Quantum mechanics and shell-model theory permit nuclear scientists to compute the transition probability (rate of decay) between nuclear states. For nuclei whose structure can be described by a small number of valence nucleons outside filled shells, the Shell Model calculations agree very well with measured values of spin and parity assignments and transition probabilities.
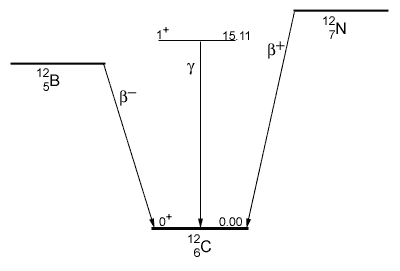
An example of transitions between a nucleus’s energy levels is shown above. The ground states of 12B (5 protons, 7 neutrons) and 12N (7 protons, 5 neutrons) are related to each other and to the 15.1 MeV state in 12C. Each has a nucleon in the third energy level, each has the quantum number 1+, 1, and each decays to the ground state of carbon. The boron and nitrogen beta decay emit an e- and e+ respectively. The 15.1 MeV state in carbon decays by gamma emission. The shell model calculations of these transition probabilities agree quite well with the measured rates even though different decay mechanisms are at work in each case. Nuclear theorists keep refining the shell model to understand the details of nuclear structure and to make that knowledge available for applications in nuclear technology.
|
|

