BERKELEY, CA—James Sethian, head of the Mathematics Group at the U.S. Department of Energy's Lawrence Berkeley National Laboratory and a professor of mathematics at the University of California at Berkeley, has been awarded the Norbert Wiener Prize in Applied Mathematics by the American Mathematical Society (AMS) and the Society for Industrial and Applied Mathematics (SIAM).

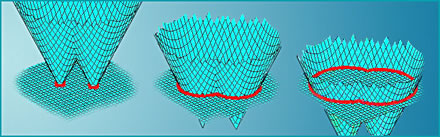
The level set method developed by James Sethian represents a front propagating in n dimensions as a level set of an object in (n + 1) dimensions, allowing curvatures and normals to be easily evaluated and topological changes to occur in a natural manner.

The prize, which was presented on January 8 at the joint AMS-SIAM meeting in Phoenix, is awarded "for an outstanding contribution to applied mathematics in the highest and broadest sense." Sethian's award marks the eighth time the Norbert Wiener Prize has been awarded since 1970. The prize was last awarded in 2000, when one of the two recipients was Alexandre Chorin, a colleague of Sethian's who also has a joint appointment in Berkeley Lab's Mathematics Group and UC Berkeley's Math Department.

"This recognition by the nation's two leading mathematical societies is a powerful testimonial to the quality and influence of James's work," said Horst Simon, director of the Computational Research Division, where Sethian's group resides. "Applied mathematics is at the heart of our computational science program, and the research by James and his group members helps advance science at Berkeley Lab and at universities and national labs across the country and around the world."

According to information distributed at the AMS-SIAM meeting awards ceremony, Sethian was honored "for his seminal work on the computer representation of the motion of curves, surfaces, interfaces, and wave fronts, and for his brilliant applications of mathematical and computational ideas to problems in science and engineering."

His work has influenced fields as diverse as medical imaging, seismic research by the petroleum industry, and the manufacture of computer chips and desktop printers. AMS and SIAM, noting that "Sethian's work is a shining example of what applied mathematics can accomplish to benefit science as a whole," provided the following descriptions of the work and its importance:

A particularly noteworthy aspect of Sethian's work is that he pursues his ideas from a first formulation of a mathematical model all the way to concrete applications in national laboratory and industrial settings; his algorithms are currently distributed in widely available packages. . . .

Sethian's earliest work included an analysis of the motion of flame fronts and of the singularities they develop; he found important new links between the motion of the fronts and partial differential equations. These connections made possible the development of advanced methods to describe front propagation through the solution of regularized equations on fixed grids.

Sethian (with S. Osher) extended this work through an implicit formulation, resulting in a methodology that has come to be known as the 'level set method,' because it represents a front propagating in n dimensions as a level set of an object in (n + 1) dimensions. Next, Sethian tamed the cost of working in higher dimensions by reducing the problem back down to its original dimensionality. This set of ideas makes possible the solution of practical problems of increasing importance and sophistication and constitutes a major mathematical development as well as an exceptionally useful computational tool with numerous applications. (Sethian is also the author of a book entitled Level Set Methods published by Cambridge University Press.)

Among the practical problems solved by Sethian are: the tracking of interfaces and drops in fluid mechanics with applications to inkjet design for high-speed printers; the analysis of crystal growth (with J. Strain); and the design of optimal structures under loads (with A. Wiegmann).

Sethian's mathematical description of etching and deposition in the manufacture of computer chips has illuminated processes such as ion milling, visibility, resputter, and material-dependent etch rates; the resulting algorithms are now an indispensable part of industrial semiconductor fabrication simulations throughout the world.

His models of implicit surface motion together with fast Eikonal solvers are standard fare in medical and biomedical shape extraction . . . and they are used in hospital electron-beam scanners to quantify cardiac motion and efficiency.

Recently, Sethian (with S. Fomel) developed efficient numerical methods for simulating multiple-arrival wavefront propagation by solving Liouville-type equations; this work has direct applications in seismic imaging and geophysical inverse problems and has already been put to use by the petroleum industry.

The Berkeley Lab is a U.S. Department of Energy national laboratory located in Berkeley, California. It conducts unclassified scientific research and is managed by the University of California.

Additional information

• More about James Sethian's work
• More about Berkeley Lab's Computational Research Division, which creates computational tools and techniques that enable scientific breakthroughs by conducting applied research and development in computer science, computational science, and applied mathematics.